一个常见于数学问题中的数列,需要对题目有缜密的分析,而后便可以方便地解出答案。
*这是本博客第一篇使用 $LaTeX$ 语法的文章,如有错误还请见谅。
卡特兰数又称卡塔兰数(Catalan Number),是组合数学中一个经常出现在各种计数问题中的数列。以比利时的数学家欧仁·查理·卡塔兰(1814–1894)的名字来命名。其前几项(下标从 0 开始)为:
1,1,2,5,14,42,132,429,1430,4862,16796,58786,208012,742900, ...
1730年我国清朝时期的明安图(蒙古人)比 Catalan 更早使用了 Catalan 数,见《割圜密率捷法》。
公式
递推式:
$f(n) = \sum_{i=0}^{n-1}f(i) \times f(n-i-1)$
另类递推式:
$f(n) = \frac{f(n-1) \times (4 \times n - 2)}{n+1}$
组合式:
$f(n)= \frac{C_{2n}^{n}}{n+1}$
另类组合式:
$f(n)=C_{2n}^{n}-C_{2n}^{n-1}$
应用
卡特兰数常见于下列问题:
- 连乘括号化
- 出栈次序
- 凸多边形三角形划分
- 给定节点组成二叉树
- $n$ 对括号正确匹配
下面是三道经典的例题:
二叉树的计数
问题描述
已知一棵二叉树有 $n$ 个节点,问:该二叉树能组成多少种不同的形态?
解题思路
设二叉树左子树节点数为 $i$,则右子树节点数为 $n-i-1$。
又设 $n$ 个节点的二叉树状态数为 $f(n)$,即可得到递推式
$f(n)=\sum_{i=0}^{n-1}f(i) \times f(n-i-1)$
答案是卡特兰数。
AB排列问题
问题描述
有 $n$ 个 A 和 $n$ 个 B 排成一排,从第一个位置开始到任何位置,B 的个数不能超过 A 的个数,问:这样的排列有多少种?
$n=1$ 时:AB,$f(1)=1$
$n=2$ 时:AABB ABAB,$f(2)=2$
$n=3$ 时:AAABBB AABBAB ABAABB ABABAB,$f(3)=5$
解题思路
即出栈次序问题。
如下图,上箭头表示 A,下箭头表示 B,递推得出结论为卡特兰数。
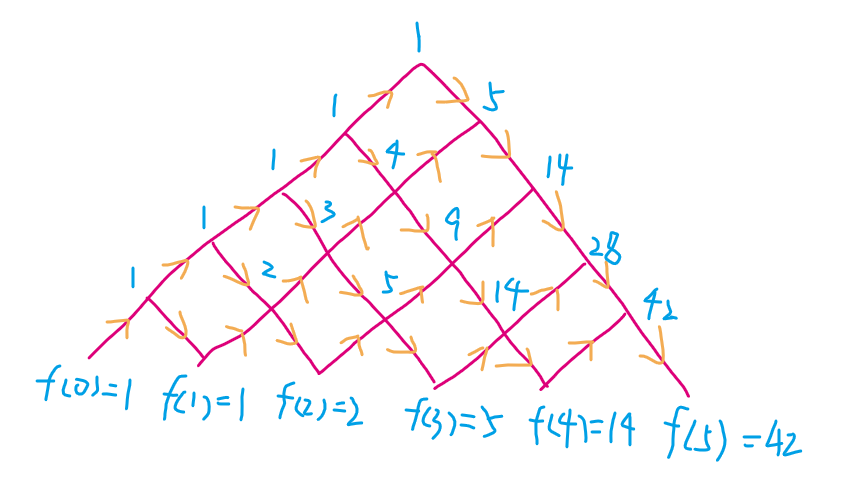
[NOI 1988]乘法加括号
问题描述
对于连乘 $a_0\times a_1\times a_2\times …\times a_n$,加了括号后可改变它的运算顺序。问:有多少种不同的运算顺序?
解题思路
将连乘表示为一棵二叉搜索树,将 “$\times$” 作为节点,得到组合方案数为 $f(0) \times f(n-1)+ f(1) \times f(n-2)+…+f(n-1) \times f(0)$
同 二叉树的计数
参考资料
《信息学奥赛之数学一本通》 林厚从