【学习笔记】树状数组

发表于 | 分类于 | 误人子弟 176个
字数统计: 1,861 | 阅读时长 ≈ 9

感觉是个好大的坑wa…我就简略地写写好了…其实树状数组在大部分时候仅作为线段树的替代品（执行的基本操作相似，且代码简单易懂，时空复杂度均低于线段树），那那那为什么需要线段树呢？树状数组的适用范围小啊（很小很小啊）执行基本修改查询操作已经很不错了还苛求什么呢…

概念与基本性质

树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和，但是每次只能修改一个元素的值；经过简单修改可以在log(n)的复杂度下进行范围修改，但是这时只能查询其中一个元素的值(如果加入多个辅助数组则可以实现区间修改与区间查询)。

——以上内容摘自百度百科

举个栗子：
设原数组为A，树状数组为C，则

C1 = A1
C2 = A1 + A2
C3 = A3
C4 = A1 + A2 + A3 + A4
C5 = A5
C6 = A5 + A6
C7 = A7
C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
…
C16 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8 + A9 + A10 + A11 + A12 + A13 + A14 + A15 + A16

观察下图：

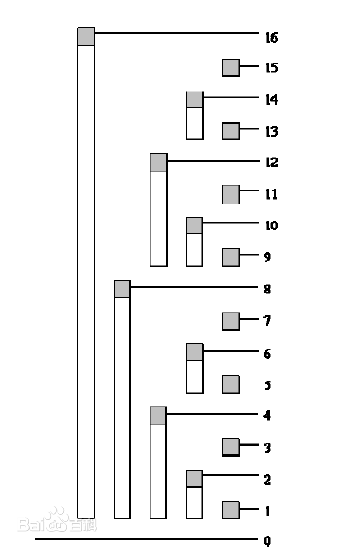
Cg8RqH.png

我们可以发现，i 号节点管辖的范围是 2 ^ k（k 是 i 的二进制末尾 0 的个数），区间最后一个元素必然是 Ai
显然，Cn=A(n – 2 ^ k + 1) + … + An

那么，问题来了：
如何求出 2 ^ k 的值呢？

这时需要引进一个特殊的函数 lowbit( )…lowb…it..（ 卡在奇怪的地方.jpg ）

1
2
3
int lowbit(int x){
    return x & (-x);
}

这个函数 巧妙 地利用了机器补码的特性，计算出了 x 二进制最低位 1 所代表的值，即 2 ^ k 的值。

然后我们就可以借助它 偷税 愉悦地完成接下来的操作了！！

执行操作

单点修改，区间查询

最基础的树状数组

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include<cstdio>
#define re register int
#define rep(i,a,b) for(re i=a;i<=b;++i)
#define ll long long
int n,m,t[2000010];
inline ll read(){
    ll f=1,x=0;char ch=getchar();
    while(ch>'9' or ch<'0'){if(ch=='-')f=-1;ch=getchar();}
    while(ch<='9' and ch>='0'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
inline int lowbit(int x){      //x 二进制最低位 1 所对应的值
    return x &(-x);
}
inline void add(int x,int k){       //单点修改
    while(x<=n){
        t[x]+=k;
        x+=lowbit(x);
    }
}
inline int sum(int x){       //前缀和
    int ans=0;
    while(x){
        ans+=t[x];
        x-=lowbit(x);
    }
    return ans;
}
inline int ask(int l,int r){      //区间查询
    return sum(r)-sum(l-1);
}
int main(){
    n=read(),m=read();
    rep(i,1,n){
        int x;
        x=read();
        add(i,x);
    }
    rep(i,1,m){
        int opt,l,r;
        opt=read(),l=read(),r=read();
        switch(opt){
            case 1:
                add(l,r);
                break;
            case 2:
                printf("%d\n",ask(l,r));
                break;
        }
    }
    return 0;
}

例题

洛谷 P3374 【模板】树状数组 1

区间修改，单点查询

其实树状数组本身并不支持区间修改，但是运用 人类智慧 我们可以发现通过差分数组（d[ i ] = a[ i ] - a[ i - 1 ] , a[ 0 ] = 0）可以将问题转换为单点修改，区间查询

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <cstdio>
#define re register int
#define rep(i,a,b) for(re i=a;i<=b;++i)
#define ll long long
inline ll read(){
    ll f=1,x=0;char ch=getchar();
    while(ch>'9' or ch<'0'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0' and ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return f*x;
}
inline int lowbit(int x){
    return x & (-x);
}
ll t[500050];
int n,m;
inline void add(int x,ll k){
    while(x<=n){
        t[x]+=k;
        x+=lowbit(x);
    }
}
inline ll val(int x){
    ll ans=0;
    while(x){
        ans+=t[x];
        x-=lowbit(x);
    }
    return ans;
}
//看起来和上一种操作没什么不同啊
int main(){
    n=read(),m=read();
    ll now,tmp=0;
    rep(i,1,n){
        now=read();
        add(i,now-tmp);      //重点在这，每次存的数都是差分后的
        tmp=now;
    }
    rep(i,1,m){
        int opt;
        opt=read();
        switch(opt){
            case 1:
                int x,y,k;
                x=read(),y=read(),k=read();
                add(x,k);
                add(y+1,-k);         //只需修改区间两端（中间差值不变）
                break;
            case 2:
                int z;
                z=read();
                printf("%lld\n",val(z));
                break;
        }
    }

    return 0;
}

例题

洛谷 P3368 【模板】树状数组 2

区间修改，区间查询

这是树状数组最常用的操作，也是用线段树最难打的（怕是常用的原因）
我们参考区间修改，单点查询的操作，只要求出val()函数的前缀和，就可以实现复杂度为 O( log n )的区间查询了

设原数组为 a，d 为 a 的差分数组，欲求 a 的前缀和

a[ 1 ] + a[ 2 ] + a[ 3 ] + … + a[ n ]
= (d[ 1 ]) + (d[ 1 ] + d[ 2 ]) + (d[ 1 ] + d[ 2 ] + d[ 3 ]) + … +(d[ 1 ] + d[ 2 ] + … + d[ n ])
= d[ 1 ] · n + d[ 2 ] · (n - 1) + … +d[ n ]
= n · (d[ 1 ] + d[ 2 ] + … +d[ n ]) - (0 · d[ 1 ] + 1 · d[ 2 ] + … + (n - 1) · d[ n ])

所以我们还要再维护一个 d2，使 d2[ i ] = (i - 1) · d[ i ]，每当修改 d 时就修改一下 d2，复杂度就不会改变

代码实现

就不用什么注释了…吧？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <cstdio>
#define re register int
#define rep(i,a,b) for(re i=a;i<=b;++i)
typedef long long ll;
ll i,j,n,m,a[200050],c[200050],c2[200050],x,l,r,w,ans;
inline ll read(){
    ll f=1,x=0;char ch=getchar();
    while(ch>'9' or ch<'0'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0' and ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return f*x;
}
inline ll lowbit(ll x){
    return x & (-x);
}
inline void add(ll x,ll w){
    for(;x<=n;x=x+lowbit(x))
        c[x]=c[x]+w;
}
inline void add2(ll x,ll w){
    for(;x<=n;x=x+lowbit(x))
        c2[x]=c2[x]+w;
}
inline ll val(ll x){
    ll ans=0;
    for(;x>0;x=x-lowbit(x))
        ans=ans+c[x];
    return ans;
}
inline ll val2(ll x){
    ll ans=0;
    for(;x>0;x=x-lowbit(x))
        ans=ans+c2[x];
    return ans;
}
int main(){
    n=read();
    rep(i,1,n){
        a[i]=read();
        add(i,a[i]-a[i-1]);
        add2(i,(i-1)*(a[i]-a[i-1]));
    }
    m=read();
    rep(i,1,m){
        x=read();
        if(x==1){
            l=read(),r=read(),w=read();
            add(l,w);
            add(r+1,-w);
            add2(l,w*(l-1));
            add2(r+1,-w*r);
        }
        else{
            l=read(),r=read();
            ans=r*val(r)-val2(r);
            ans=ans-((l-1)*val(l-1)-val2(l-1));
            printf("%lld\n",ans);
        }
    }
    return 0;
}

例题

CodeVS 1082 线段树练习 3
为什么难度是大师啊喂

二维树状数组

当然，树状数组这么有用（代码量小）的数据结构，怎么会少了矩阵呢？为什么我要新开一个标题啊…

在一维树状数组中，tree[ x ] 记录的是右端点为 x、长度为 lowbit( x ) 的区间的区间和。
那么在二维树状数组中，可以类似地定义 tree[ x ][ y ] 记录的是右下角为 (x, y)，高为 lowbit( x ), 宽为 lowbit( y ) 的区间的区间和。

嘛，具体操作什么的（我好懒啊）前两种很好懂啊… 自己找度娘吧
至于区间修改 + 区间查询，可以参考我写的 【题解】上帝造题的七分钟（二维树状数组）

那…就写到这吧。

0%