【学习笔记】莫队算法

发表于 | 分类于 | 误人子弟 个
字数统计: 1,003 | 阅读时长 ≈ 5

算法介绍

莫队算法，简单说就是基于分块进行暴力

莫队算法，是由前国家队队长莫涛在役时创造的，为数不多几种在役选手在比赛或平时训练中创造并广为流传使用的算法之一。

此算法在OI界具有极高的人气，据说能解决一切区间处理问题，当然我这种蒟蒻却只能板子题做做，让我们通过下面的题目简单了解一下莫队算法。

题意简述

有 n 个物品，分属于不同的类别，给出m个区间，求在各个区间中连续两次取出相同类别的物品的概率，最简分数表示，若概率为0则输出0/1。（n,m<=50000）

思路

首先，我们需要两个指针 l 和 r 来指示当前区间的位置，用 sum[ ] 数组存放当前区间各类别数量，ans 为区间结果，ans 的分母是所有的组合数 (r - l + 1) (r - l)，而分子是各个类别的sum[ ]的平方的累加和，根据其中任意一个区间的 ans 求出相邻区间的 ans。

这里相邻区间定义为当前区间的 l - 1 或 l + 1 或 r - 1 或 r + 1
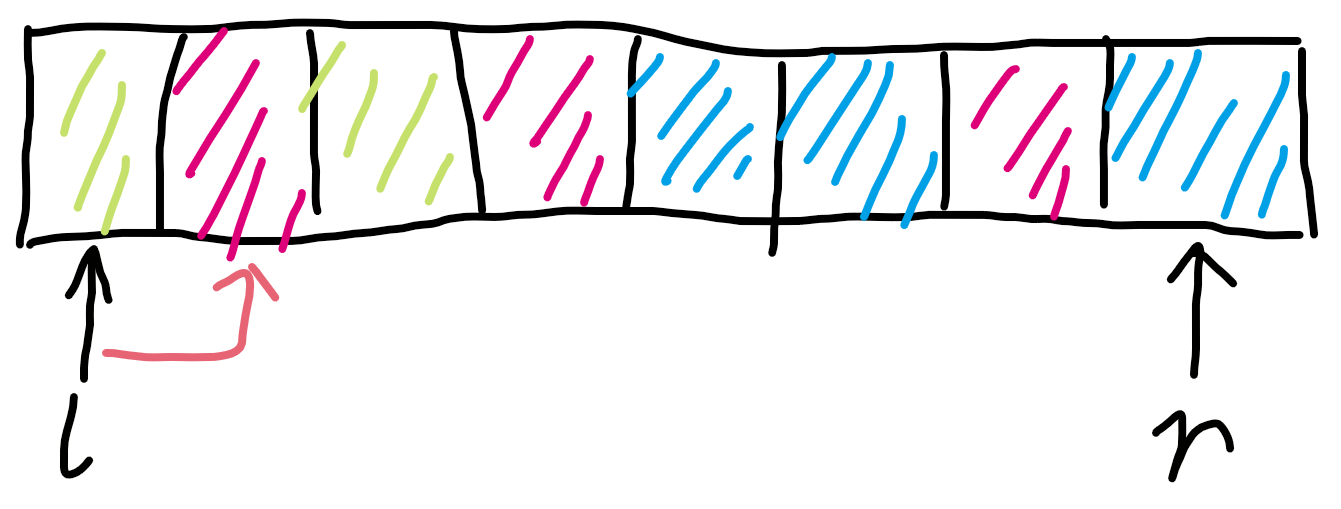
以 l + 1 为例，如下图：
C0oiGD.png
我们将 l + 1,此时 sum[green] - 1，区间总数也 - 1，这时你会发现改变一次的时间复杂度竟然是O( 1 )？！
其他的改变也是同理

当然这样是远远不够的，若是逐个区间暴力枚举，复杂度是O( n ^ 2 )，太高了呀
这时需要引入变量 unit = sqrt( n )，用它来进行分块（将 n 分为 sqrt( n ) 个区域），并用 ad[ i ] 来存储 i 所在的区间，这样，进行指针跳动时，最多只需要 2 * sqrt( n ) 次就能到达目标，大大优于之前的 n 次。

最后再次致敬莫涛大神！！

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include<cstdio>
#include<cmath>
#include<algorithm>
#define re register int
#define rep(i,a,b) for(re i=a;i<=b;++i)
#define ll long long
#define MAXN 50050
using namespace std;
inline ll read(){
    int f=1,x=0;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*=f;
}
inline ll gcd(ll m,ll n){while(m>0){ll c=n%m;n=m;m=c;}return n;}
inline ll pow2(ll x){return x*x;}
struct Mo{ll l,r,cnt;ll A,B;}ask[MAXN];   //存储区间信息
//A,B分别存储结果的分子和分母
ll n,m,col[MAXN],unit,ad[MAXN];
ll sum[MAXN],ans=0;
inline bool cmp1(Mo a,Mo b){    //优化时间复杂度
	return ad[a.l]==ad[b.l]?a.r<b.r:a.l<b.l;
}       //左指针为第一关键字
inline bool cmp2(Mo a,Mo b){return a.cnt<b.cnt;}
inline void revise(int x,int add){     //每次改变并维护ans和sum[ ]
	ans-=pow2(sum[col[x]]);
	sum[col[x]]+=add;
	ans+=pow2(sum[col[x]]);
}
int main(){
	n=read(),m=read();
	unit=sqrt(n);
	rep(i,1,n){
		col[i]=read();
		ad[i]=i/unit+1;     //分块
	}
	rep(i,1,m){
		ask[i].l=read(),ask[i].r=read();
		ask[i].cnt=i;          //记录原顺序
	}
	sort(ask+1,ask+m+1,cmp1);     //减少指针总变换次数
	int l=1,r=0;
	rep(i,1,m){   //执行操作
		while(l<ask[i].l) revise(l,-1),++l;
		while(l>ask[i].l) revise(l-1,1),--l;
		while(r<ask[i].r) revise(r+1,1),++r;
		while(r>ask[i].r) revise(r,-1),--r;
		if(ask[i].l==ask[i].r){      //输出0/1
			ask[i].A=0;
			ask[i].B=1;
			continue;
		}
		ask[i].A=ans-(ask[i].r-ask[i].l+1);
		ask[i].B=(ask[i].r-ask[i].l+1)*(ask[i].r-ask[i].l);
		ll tmp=gcd(ask[i].A,ask[i].B);     //最简
		ask[i].A/=tmp;
		ask[i].B/=tmp;
	}
	sort(ask+1,ask+m+1,cmp2);     //按照原排序输出
	rep(i,1,m)
		printf("%lld/%lld\n",ask[i].A,ask[i].B);

	return 0;
}

题目来源

BZOJ 2038 [2009国家集训队]小Z的袜子(hose)

0%